Potencial de Coulomb
La ley de Coulomb establece que la presencia de una carga puntual general induce en todo el espacio la aparición de un campo de fuerzas que decae según la ley de la inversa del cuadrado. Para modelizar el campo debido a varias cargas eléctricas puntuales estáticas puede usarse el principio de superposición
dada la aditividad de las fuerzas sobre una partícula. Sin embargo,
matemáticamente el manejo de expresiones vectoriales de ese tipo puede
llegar a ser complicado, por lo que frecuentemente resulta más sencillo
definir un potencial eléctrico. Para ello a una carga puntual
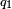
se le asigna una función escalar o
potencial de Coulomb 
tal que la fuerza dada por la ley de Coulomb sea expresable como:

De la ley de Coulomb se deduce que la función escalar que satisface la anterior ecuación es:
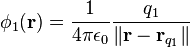
Donde:
 , es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
, es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
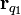
, es el vector de posición de la carga eléctrica

cuyo campo pretende caracterizarse por medio del potencial.

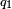 se le asigna una función escalar o potencial de Coulomb
se le asigna una función escalar o potencial de Coulomb  tal que la fuerza dada por la ley de Coulomb sea expresable como:
tal que la fuerza dada por la ley de Coulomb sea expresable como: , es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
, es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y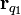 , es el vector de posición de la carga eléctrica
, es el vector de posición de la carga eléctrica  cuyo campo pretende caracterizarse por medio del potencial.
cuyo campo pretende caracterizarse por medio del potencial.
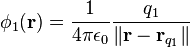
No hay comentarios:
Publicar un comentario